1.
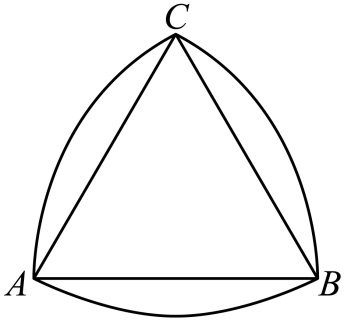
已知 是边长为2的等边三角形.如图,将
是边长为2的等边三角形.如图,将 的顶点
的顶点 与原点重合,
与原点重合, 在
在 轴上,然后将三角形沿着
轴上,然后将三角形沿着 轴正方向滚动,每当顶点
轴正方向滚动,每当顶点 再次回落到
再次回落到 轴上时,将相邻两个点
轴上时,将相邻两个点 之间的距离称为“一个周期”,则完成“一个周期”时,顶点
之间的距离称为“一个周期”,则完成“一个周期”时,顶点 的路径长度为.
的路径长度为.

【考点】
扇形的弧长与面积;