1.
我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.
(1)
在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美"四边形的是(请填序号);
(2)
在“完美”四边形 中,
中, ,
,  , 连接
, 连接 .
.


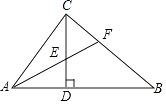
①如图1,求证:平分
;
小明通过观察、实验,提出以下两种想法,证明平分
:
想法一:通过 , 可延长
到
, 使
, 通过证明
, 从而可证
平分
;
想法二:通过 , 可将
绕点
顺时针旋转,使
与
重合,得到
, 可证
,
,
三点在一条直线上,从而可证
平分
.
请你参考上面的想法,选择其中一种想法帮助小明证明平分
;
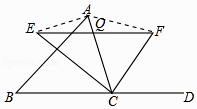
②如图2,当时,用等式表示线段
,
,
之间的数量关系,并证明.
【考点】
角平分线的性质;
等腰三角形的判定与性质;