1.
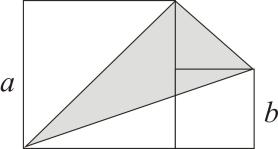
如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积,并求当 时代数式的值是多少.
时代数式的值是多少.
【考点】
三角形的面积;
矩形的性质;
正方形的性质;