1.
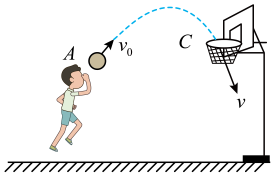
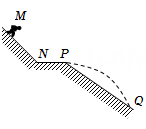
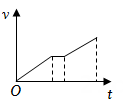
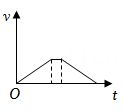
达·芬奇的手稿中描述了这样一个实验:一个罐子在空中沿水平直线向右做匀加速运动,沿途连续漏出沙子。若不计空气阻力,则下列图中能反映空中沙子排列的几何图形是( )
A.
 B.
B.
 C.
C.
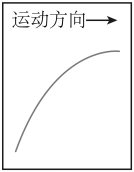 D.
D.
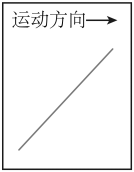
 B.
B.
 C.
C.
 D.
D.

【考点】
运动的合成与分解;
能力提升
变式训练
拓展培优
真题演练