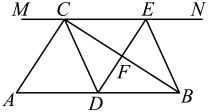
如图，在Rt△ABC中，∠ACB=90°，过点C的直线， D为AB边上一点，过点D作DE⊥BC，垂足为F，交直线MN于E，连接CD，BE．

1. 如图，在Rt△ABC中，∠ACB=90°，过点C的直线 $\text{[math]}$ ， D为AB边上一点，过点D作DE⊥BC，垂足为F，交直线MN于E，连接CD，BE．

(1) 求证：CE=AD：

(2) 当D为AB中点时，证明：四边形BECD是菱形．

(3) 在满足（2）的条件下，当△ABC满足条件时，四边形BECD是正方形．

【考点】

平行四边形的判定与性质; 菱形的判定; 正方形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点C的直线 $\text{[math]}$ ， D为 $\text{[math]}$ 边上一点，过点D作 $\text{[math]}$ ，交直线 $\text{[math]}$ 于E，垂足为F，连接 $\text{[math]}$ 、 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 当D在 $\text{[math]}$ 中点时，四边形 $\text{[math]}$ 是什么特殊四边形？请说明你的理由；

(3) 若D为 $\text{[math]}$ 中点，则当 $\text{[math]}$ 的大小满足什么条件时，四边形 $\text{[math]}$ 是正方形？请说明你的理由．

综合题普通

2. 如图，点E、F分别在▱ABCD的边AB、CD的延长线上，且BE＝DF，连接AC、EF、AF、CE，AC与EF交于点O.

(1) 求证：AC、EF互相平分；

(2) 若EF平分∠AEC，求证：四边形AECF是菱形.

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 的中点，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 为平行四边形；

(2) 请对 $\text{[math]}$ 的边或角添加一个条件，使得四边形 $\text{[math]}$ 成为菱形，并进行证明．

综合题普通