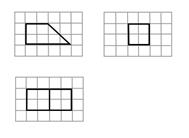
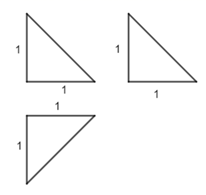
棱锥的内切球半径，其中，分别为该棱锥的体积和表面积，如图为某三棱锥的三视图，若每个视图都是直角边长为的等腰直角形，则该三棱锥内切球半径为（）

1. 棱锥的内切球半径 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ 分别为该棱锥的体积和表面积，如图为某三棱锥的三视图，若每个视图都是直角边长为 $\text{[math]}$ 的等腰直角形，则该三棱锥内切球半径为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

由三视图求面积、体积;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 某几何体的三视图如图所示（单位： $\text{[math]}$ ），则该几何体的体积（单位： $\text{[math]}$ ）是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 已知某几何体的三视图如图所示，三个视图的外轮廓为矩形和正方形，则该几何体的侧面面积最大的面的面积为（）

A. 9 B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 某几何体的三视图如图所示（单位： $\text{[math]}$ ），则该几何体的表面积（单位： $\text{[math]}$ ）是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. 3π D. $\text{[math]}$

单选题容易