1.
 和
和 都是等腰直角三角形,
都是等腰直角三角形, .
.

(1)
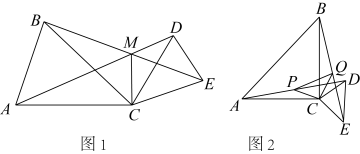
如图1,点D、E在 ,
,  上,则
上,则 ,
,  满足怎样的数量关系和位置关系?(直接写出答案不证明)
(2)
如图2,点D在
满足怎样的数量关系和位置关系?(直接写出答案不证明)
(2)
如图2,点D在 内部,点E在
内部,点E在 外部,连接
外部,连接 ,
,  , 则
, 则 ,
,  满足怎样的数量关系和位置关系?请说明理由.
满足怎样的数量关系和位置关系?请说明理由.
【考点】
等腰直角三角形;
三角形全等的判定-SAS;
能力提升
真题演练