1.
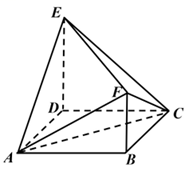
足球起源于中国古代的蹴鞠游戏.“蹴”有用脚蹴、踢的含义,“鞠”最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,已知某“鞠”的表面上有四个点 , 满足
, 满足 ,
,  面ABC,
面ABC, ⊥
⊥ , 若
, 若 , 则该“鞠”的体积的最小值为( )
, 则该“鞠”的体积的最小值为( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
棱柱、棱锥、棱台的体积;
基础巩固
能力提升
变式训练
拓展培优
真题演练