1.
综合与实践
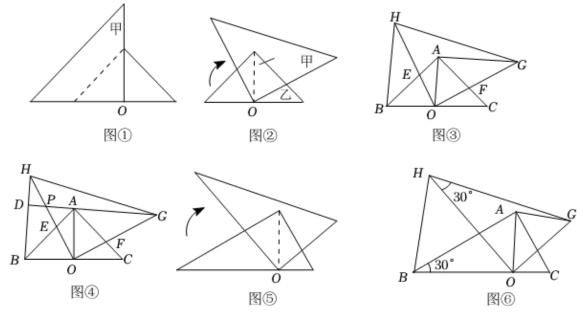
九年级(1)班同学在数学老师的指导下,以“三角形的旋转”为主题,开展数学活动.
(1)
操作探究:
(2)
迁移探究:
(3)
拓展应用:

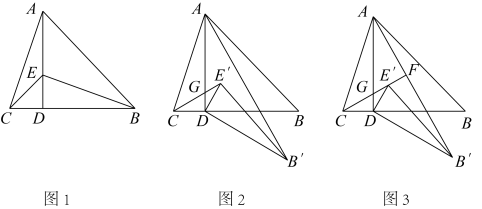
如图1,为等边三角形,将
绕点
旋转
, 得到
, 连接
, 则
. 若
是
的中点,连接
, 则
与
的数量关系是.
如图2,(1)中的其他条件不变,当绕点
逆时针旋转
, 得到
, 求出此时
的度数及
与
的数量关系.
如图3,在中,
,
, 将
绕点
旋转,得到
, 连接
,
是
的中点,连接
. 当
时,求
的长.
【考点】
旋转的性质;
三角形的综合;
能力提升
真题演练