1.
综合与实践
综合实践课上,老师让同学们以“三角形纸片的折叠”为主题开展数学活动.

(1)
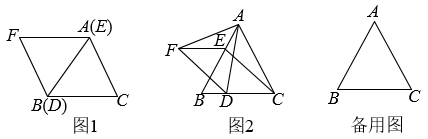
【操作发现】对折 , 使点
, 使点 落在边
落在边 上的点
上的点 处,得到折痕
处,得到折痕 , 把纸片展平,如图
, 把纸片展平,如图 小明根据以上操作发现:四边形
小明根据以上操作发现:四边形 满足
满足 ,
,  查阅相关资料得知,像这样的有两组邻边分别相等的四边形叫作“筝形”
查阅相关资料得知,像这样的有两组邻边分别相等的四边形叫作“筝形” 请写出图
请写出图 中筝形
中筝形 的一条性质 .
(2)
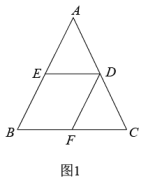
【探究证明】如图
的一条性质 .
(2)
【探究证明】如图 , 连接
, 连接 , 设筝形
, 设筝形 的面积为
的面积为 若
若 , 求
, 求 的最大值;
(3)
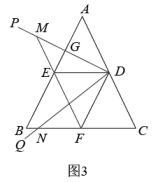
【迁移应用】在
的最大值;
(3)
【迁移应用】在 中,
中, ,
,  ,
,  , 点
, 点 ,
,  分别在
分别在 ,
,  上,当四边形
上,当四边形 是筝形时,请直接写出四边形
是筝形时,请直接写出四边形 的面积.
的面积.
【考点】
三角形的综合;
能力提升
真题演练