1.
奇奇在学习了圆柱的表面积后又如下思考:
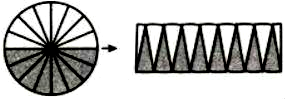
要计算圆柱的表面积,需要计算圆柱的侧面积加上下两个底面的面积。圆柱的侧面沿高度展开是一个长方形。回顾圆的面积推导过程,圆的面积也可以转化成近似的长方形,那么圆柱的表面积可不可以转化成一个大的长方形的面积呢?
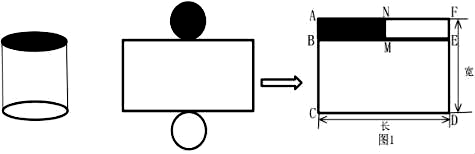
如图是奇奇的操作过程,按照奇奇的方法,请你完成下面的思考过程:
回顾圆的面积推导过程,图1中,黑色小长方形ABMN的宽是圆柱底面的,大长方形ACDF的宽等于圆柱的加圆柱底面的,大长方形ACDF的长是圆柱底面的。
因为长方形的面积=长×宽,所以圆柱的表面积=×。
【考点】
圆柱的侧面积、表面积;
基础巩固
能力提升
变式训练
拓展培优
真题演练






