1.
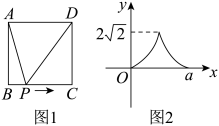
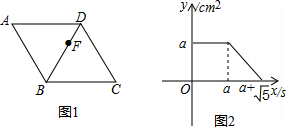
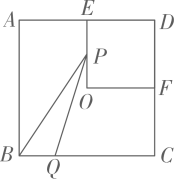
如图,四边形 是边长为
是边长为 的正方形,点E,点F分别为边
的正方形,点E,点F分别为边 ,
,  中点,点O为正方形的中心,连接
中点,点O为正方形的中心,连接 , 点P从点E出发沿
, 点P从点E出发沿 运动,同时点Q从点B出发沿
运动,同时点Q从点B出发沿 运动,两点运动速度均为
运动,两点运动速度均为 , 当点P运动到点F时,两点同时停止运动,设运动时间为
, 当点P运动到点F时,两点同时停止运动,设运动时间为 , 连接
, 连接 ,
,  的面积为
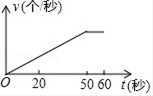
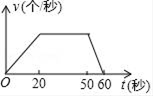
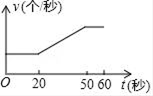
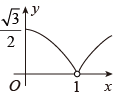
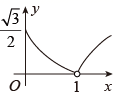
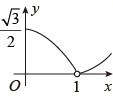
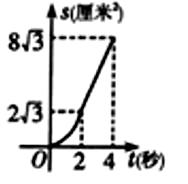
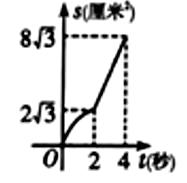
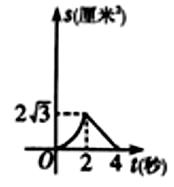
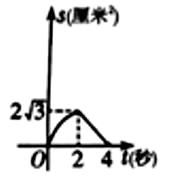
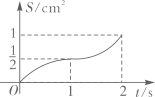
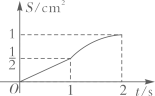
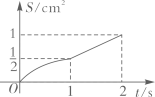
的面积为 , 下列图像能正确反映出S与t的函数关系的是( )
, 下列图像能正确反映出S与t的函数关系的是( )
A.
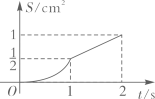 B.
B.
 C.
C.
 D.
D.
 B.
B.
 C.
C.
 D.
D.

【考点】
动点问题的函数图象;
四边形-动点问题;