1.
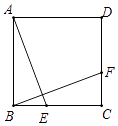
问题背景：在正方形ABCD的外侧，作△ADE和△DCF，连接AF，BE．
(1)
特例探究：如图1，若△ADE和△DCF均为等边三角形，试判断线段AF与BE的数量关系和位置关系，并说明理由；
(2)
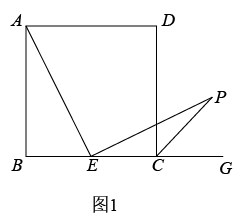
拓展应用：如图2，在△ADE和△DCF中，
， 
， 且
， 求四边形ABFE的面积？
【考点】
三角形全等的判定;
正方形的性质;
