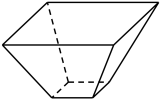
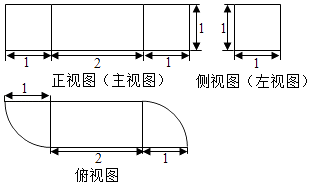
某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：）是（）

1. 某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位： $\text{[math]}$ ）是（）

A. 1 B. $\text{[math]}$ C. 2 D. $\text{[math]}$

【考点】

组合几何体的面积、表面积、体积问题; 由三视图还原几何体;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍童.如图池盆几何体是一个刍童，其中上下底面为正方形边长分别为6和2，侧面是全等的等腰梯形梯形的高为 $\text{[math]}$ ，若盆中积水深为池盆高度的一半，则该盆中积水的体积为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 如图，将一个圆柱 $\text{[math]}$ 等分切割，再将其重新组合成一个与圆柱等底等高的几何体， $\text{[math]}$ 越大，重新组合成的几何体就越接近一个“长方体”．若新几何体的表面积比原圆柱的表面积增加了10，则圆柱的侧面积为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，何尊是我国西周早期的青铜礼器，其造型浑厚，工艺精美，尊内底铸铭文中的“宅兹中国”为“中国”一词最早的文字记载，何尊还是第一个出现“德”字的器物，证明了周王朝以德治国的理念，何尊的形状可近似看作是圆台和圆柱的组合体，组合体的高约为 $\text{[math]}$ ，上口直径约为 $\text{[math]}$ ，经测量可知圆台的高约为 $\text{[math]}$ ，圆柱的底面直径约为 $\text{[math]}$ ，则该组合体的体积约为（）（其中 $\text{[math]}$ 的值取 $\text{[math]}$ ， $\text{[math]}$ ）

A. $\text{[math]}$ B. $\text{[math]}$ $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易