1.
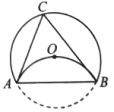
如图, 的半径为6,将劣弧沿弦
的半径为6,将劣弧沿弦 翻折,恰好经过圆心
翻折,恰好经过圆心 , 点
, 点 为优弧
为优弧 上的一个动点,则
上的一个动点,则 面积的最大值是( )
面积的最大值是( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
圆-动点问题;