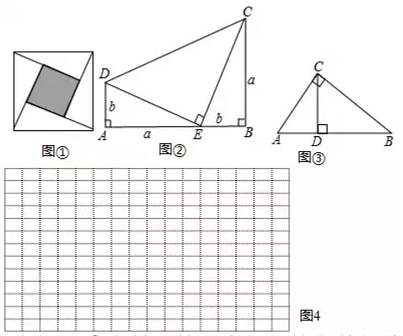
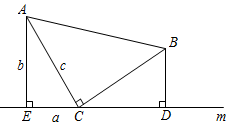
勾股定理被誉为“几何明珠”，在数学的发展历程中占有举足轻重的地位.它是初中数学中的重要知识点之一，也是初中学生以后解决数学问题和实际问题中常常运用到的重要知识，因此学好勾股定理非常重要.学习数学“不仅要知其然，更要知其所以然”，所以，我们要学会勾股定理的各种证明方法.请你利用如图图形证明勾股定理：已知：如图，四边形ABCD中，BD⊥CD，AE⊥BD于点E，且△ABE≌△BCD. 求证：AB2＝BE2+AE2.

1. 勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图2摆放时，都可以用“面积法”来证明，请你利用图2证明勾股定理（其中∠DAB＝90°）求证：a²+b²＝c².

证明题普通

2. 如图，在△ABC中，∠C＝90°，AD是BC边上的中线，DE⊥AB，垂足为E，

求证：AC²＝AE²－BE² ．

证明题普通

3. 勾股定理神秘而美妙，它的证法多样，其中的“面积法”给了李明灵感，他惊喜地发现；当两个全等的直角三角形如图（1）摆放时可以利用面积法”来证明勾股定理，过程如下

如图（1）∠DAB=90°，求证：a²+b²=c²

证明：连接DB，过点D作DF⊥BC交BC的延长线于点F，则DF=b-a

S_四边形_ADCB= $\text{[math]}$

∴ $\text{[math]}$ 化简得：a²+b²=c²

请参照上述证法，利用“面积法”完成如图（2）的勾股定理的证明，如图（2）中∠DAB=90°，求证：a²+b²=c²

证明题普通

1. 到目前为止勾股定理的证明方法已约有500种，这些证法融几何知识与代数知识于一体，完美地体现了数形结合的魅力．如图所示可以用来验证勾股定理的有（）

A. 1个 B. 2个 C. 3个 D. 4个

单选题普通

2. 勾股定理是数学定理中证明方法最多的定理之一，也是用代数思想解决几何问题的最重要的工具之一，下列图形中可以证明勾股定理的有（）

A. ①②③ B. ②③④ C. ①②④ D. ①③④

单选题容易

3. 在勾股定理的学习过程中，我们已经学会了运用如下图形，验证著名的勾股定理，这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”.实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律，它体现的数学思想是（）

A. 统计思想 B. 分类思想 C. 数形结合思想 D. 方程思想

单选题容易

1. 勾股定理是证明方法最多的定理之一，小明便以此建立项目，加以探究.

【问题提出】小明在做作业本时发现利用右图可以证明勾股定理.思路为利用面积法，将梯形的面积用不同的方式表示列出等式.由此猜想如果将Rt△DAF向左平移，能否证明勾股定理？

【方案设计】考虑到探究的难度，他首先设计了两种特殊的位置，开展研究：

方案	方案一	方案二
图形
备注	Rt△BCA≌Rt△EAD	Rt△BCA≌Rt△CFD
备注	BC=a，AC=b，AB=c

(1) 【探究验证】首先验证方案一为方案二提供经验基础.

方式

验证过程

（分别用含有a，b，c的代数式完成填空）

图形

方式①

S_{四边形ADBE}=S_△_ABE+S_△_ABD

S△ABE= ▲ ．（以AE为底，高为BC）

S△ABD= ▲ ．（以AD为底，则AD边上的高与AC等长）

连结BE，BD，不难得出AB⊥ED

方式②

S_{四边形ADBE}=S_△_EBD+S_△_EAD

S_△_EBD= $\text{[math]}$ EDBH，S_△_EAD=EDAH

S_△_EBD+S_△_EAD= $\text{[math]}$ EDBH＋ $\text{[math]}$ EDAH

= $\text{[math]}$ ED（BH＋AH）= $\text{[math]}$ EDAB= ▲

综上所述利用方式①，②列出等式即可证明勾股定理.

(2) 【方法应用】

根据上述经验，请你继续完成方案二后续的证明过程.提示：如图，连结BD，AD，不难得出CD⊥BA，利用两种方法表示四边形BCAD的面积.

实践探究题困难

2. 教材在探索平方差公式时利用了面积法，面积法除了可以帮助我们记忆公式，还可以直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为 $\text{[math]}$ ，较小的直角边长都为 $\text{[math]}$ ，斜边长都为 $\text{[math]}$ ），大正方形的面积可以表示为 $\text{[math]}$ ，也可以表示为 $\text{[math]}$ ，由此推导出重要的勾股定理：如果直角三角形两条直角边长为 $\text{[math]}$ ，斜边长为 $\text{[math]}$ ，则 $\text{[math]}$ ．

(1) 图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．

(2) 如图③，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的高， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

(3) 试构造一个图形，使它的面积能够解释 $\text{[math]}$ ，画在如图4的网格中，并标出字母 $\text{[math]}$ 所表示的线段．

综合题困难

3. 数与形是数学中的两个最古老，也是最基本的研究对象．数与形也是有联系的，这种联系称为“数形结合”．利用“数形结合”思想可以直观地帮助我们解决一些数学验证或运算．

(1) 我国是最早了解勾股定理的国家之一，该定理阐明了直角三角形的三边关系．请你利用如图对勾股定理（即下列命题）进行验证，从中体会“数形结合”的思想：

已知：如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ，（点B，C，D在一条直线上）， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

证明： $\text{[math]}$ ；

(2) 请利用“数形结合”思想，画图推算出 $\text{[math]}$ 的结果．

证明题普通

1. 2002年8月，在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图1），且大正方形的面积是15，小正方形的面积是3，直角三角形的较短直角边为a，较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放，那么图2中最大的正方形的面积为.

填空题普通

2. 如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH . 连结EG，BD相交于点O，BD与HC相交于点P.若GO=GP，则 $\text{[math]}$ 的值是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题困难

3. 如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE⊥直线m于点E，BD⊥直线m于点D．

①求证： $\text{[math]}$ ；

②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．

证明题普通