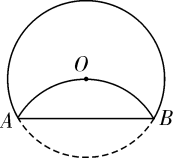
如图，公园内有一个半径为18米的圆形草坪，从地走到地有观赏路（劣弧）和便民路（线段）.已知、是圆上的点，为圆心，，小强从走到，走便民路比走观赏路少走（）米.

1. 如图，公园内有一个半径为18米的圆形草坪，从 $\text{[math]}$ 地走到 $\text{[math]}$ 地有观赏路（劣弧 $\text{[math]}$ ）和便民路（线段 $\text{[math]}$ ）.已知 $\text{[math]}$ 、 $\text{[math]}$ 是圆上的点， $\text{[math]}$ 为圆心， $\text{[math]}$ ，小强从 $\text{[math]}$ 走到 $\text{[math]}$ ，走便民路比走观赏路少走（）米.

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

垂径定理; 弧长的计算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，在扇形纸扇中，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 若扇形AOB的半径为6， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A. 2π B. 3π C. 4π D. 6π

单选题容易

3. 如图：AB是⊙O的直径，弦CD⊥AB于E，若AB＝20，CD＝16，则线段BE的长为（）

A. 4 B. 6 C. 8 D. 10

单选题容易