如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，AE∥BC ， CE∥AD ．

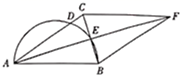
1. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，AE∥BC ， CE∥AD ．

(1) 求证：四边形ADCE是菱形；

(2) 连接BE ，若∠ABC＝30°，AC＝2，求BE的长．

【考点】

勾股定理; 菱形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

综合题普通

①当正方形PMNQ与△ABC重叠部分图形是正方形时，求t的取值范围．

②当边MN的中点落在△ABC的边上时，求正方形PMNQ的面积．

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的半圆交 $\text{[math]}$ 于点D，交 $\text{[math]}$ 于点E．延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

综合题普通