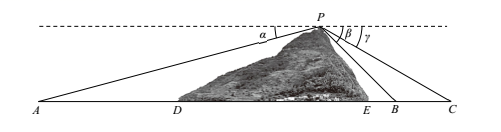
如图，，，为山脚两侧共线的三点，在山顶处观测三点的俯角分别为，， .现测得，，，，， .计划沿直线开通一条穿山隧道，试求出隧道的长度.

1. 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为山脚两侧共线的三点，在山顶 $\text{[math]}$ 处观测三点的俯角分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .现测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .计划沿直线 $\text{[math]}$ 开通一条穿山隧道，试求出隧道 $\text{[math]}$ 的长度.

【考点】

正弦定理的应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 在 $\text{[math]}$ 中，a ， b ， c分别为内角A ， B ， C的对边，且 $\text{[math]}$ ．

(1) 求角C的大小；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积．

解答题普通

2. 已知a，b，c分别为△ABC三个内角A，B，C的对边， $\text{[math]}$

(2) 若a=2，△ABC的面积为 $\text{[math]}$ ；求b，c．

解答题普通

3. 在△ABC中，2cos2A+3=4cosA．

(1) 求角A的大小；

(2) 若a=2，求△ABC的周长l的取值范围．

解答题普通