如图，点D是半径为R的⊙O上一点．

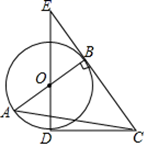
1. 如图，点D是半径为R的⊙O上一点．

(1) 若∠A＝∠C＝30°，求证：直线CD与⊙O相切；

(2) 已知直线CD与⊙O相切，下列条件：①AD＝CD；②∠A＝30°；③∠ADC＝120°；④DC＝ $\text{[math]}$ R ．其中能得出BC＝R的是哪几个？并给出你认为能得出的第一个（按编号顺序）的说理过程．

【考点】

等腰三角形的性质; 切线的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径作 $\text{[math]}$ ，点D为 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点E．

(1) 判断直线 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，通过尺规作图（作图痕迹如图所示）得到的射线与AC相交于点P ．以点P为圆心，AP为半径的圆与尺规作图得到的射线的一个交点为F ，连接AF ．

(1) 求证：BC是⊙P的切线；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的大小．

综合题普通

3. 如图，AB是⊙O的直径，P在AB的延长线上，PD与⊙O相切于D，C在⊙O上，PC＝PD.

(1) 求证：PC是⊙O的切线.

(2) 连接AC，若AC＝PC，PB＝1，求⊙O的半径.

综合题普通