如图，直线AB过点A（3，0），B（0，2）

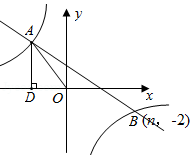
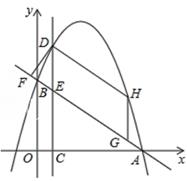
1. 如图，直线AB过点A（3，0），B（0，2）

(1) 求直线AB的解析式。

(2) 过点A作AC⊥AB且AC∶AB=3∶4，求过B、C两点直线的解析式．

【考点】

待定系数法求一次函数解析式;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 经研究表明，某市跨河大桥上的车流速度 $\text{[math]}$ （单位：千米/时）是车流密度 $\text{[math]}$ （单位：辆/千米）的函数，函数图象如图所示.

(1) 当 $\text{[math]}$ 时， $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式是______；

(2) 求车流量 $\text{[math]}$ （单位：辆/时）与车流密度 $\text{[math]}$ 之间的函数关系式；（注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量＝车流速度×车流密度）

(3) 若车流速度 $\text{[math]}$ 不低于50千米/时，求当车流密度 $\text{[math]}$ 为多少时，车流量 $\text{[math]}$ 达到最大，并求出这一最大值.

综合题普通

2. 下表是一次函数 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为常数）的自变量 $\text{[math]}$ 与函数 $\text{[math]}$ 的对应值：

$\text{[math]}$	－2	0	1
$\text{[math]}$	3	$\text{[math]}$	0

(1) 根据表格，求一次函数的解析式．

(2) 请直接写出 $\text{[math]}$ =．

综合题普通

3. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，-2）．

(1) 求直线AB的解析式；

(2) 若点C在直线AB上，且 $\text{[math]}$ ，求点C的坐标．

综合题普通