如图，正方形ABCD和正方形AEFG有公共点A，点B在线段DG上.

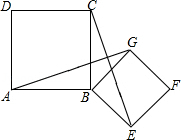
1. 如图，正方形ABCD和正方形AEFG有公共点A，点B在线段DG上.

(1) 判断DG与BE的位置关系，并说明理由：

(2) 若正方形ABCD的边长为2，正方形AEFG的边长为2 $\text{[math]}$ ，求BE的长.

【考点】

全等三角形的判定与性质; 勾股定理; 正方形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，四边形ABCD、BEFG均为正方形，连接AG、CE．

(1) 求证：AG=CE；

(2) 求证：AG⊥CE．

综合题普通

2. 勾股定理是数学史上非常重要的一个定理．早在2000多年以前，人们就开始对它进行研究，至今已有几百种证明方法．在欧几里得编的《原本》中证明勾股定理的方法如下，请同学们仔细阅读并解答相关问题：如图；分别以Rt△ABC的三边为边长，向外作正方形ABDE、BCFG、ACHI．

(1) 设正方形ABDE的面积为 $\text{[math]}$ ，正方形BCFG的面积为 $\text{[math]}$ ，正方形ACHI的面积为 $\text{[math]}$ ，证明 $\text{[math]}$ ；

(2) 连接BI、CE，求证：EC＝BI；

(3) 过点B作AC的垂线，交AC于点M，交IH于点N．试说明四边形AMNI与正方形ABDE的面积相等．

综合题普通

3. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，Q为AB的中点．动点P从点A出发沿折线AC--CB以每秒2个单位长度的速度运动，连结PQ，以PQ为边构造正方形PMNQ且边MN与点B始终在边PQ同侧．设点P的运动时间为t秒(>0)．

(1) 线段AB的长为

(2) 当点P在边AC上运动时，线段CP的长为 ▲ (用含t的代数式表示) ．

①当正方形PMNQ与△ABC重叠部分图形是正方形时，求t的取值范围．

②当边MN的中点落在△ABC的边上时，求正方形PMNQ的面积．

(3) 当点P不与点C重合时，作点C关于直线PQ的对称点C'当PC'⊥AB时，直接写出t的值．

综合题普通