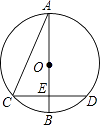
如图，以AB为直径的⊙O与弦CD相交于点E，且AC=2，AE= ，CE=1．则的长是（）

1. 如图，以AB为直径的⊙O与弦CD相交于点E，且AC=2，AE= $\text{[math]}$ ，CE=1．则 $\text{[math]}$ 的长是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

勾股定理; 勾股定理的逆定理; 垂径定理; 弧长的计算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，在 $\text{[math]}$ 中，弦AB的长为8，圆心O到AB的距离 $\text{[math]}$ ，则 $\text{[math]}$ 的半径长为（）

A. 4 B. $\text{[math]}$ C. 5 D. $\text{[math]}$

单选题容易

2. 如图是直径为 $\text{[math]}$ 的圆柱形排水管的截面示意图．若管内有积水（阴影部分），水面宽AB为 $\text{[math]}$ ，则积水的最大深度CD为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，AB是⊙O的弦，OC⊥AB于点D ，交⊙O于点C ，若半径为5，OD＝3，则弦AB的长为（　　）

A. 5 B. 6 C. 7 D. 8

单选题容易