1.
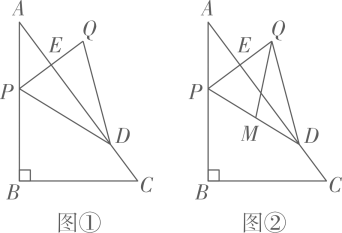
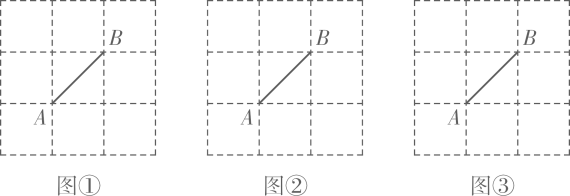
在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.

(1)
若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)
在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)
在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①;②.
【考点】
三角形相关概念;
能力提升
真题演练