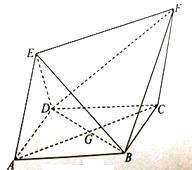
1.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=  ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.

(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A﹣DF﹣B的大小.
【考点】
直线与平面平行的判定;
与二面角有关的立体几何综合题;