若四边形的一条对角线把四边形分成两个等腰三角形，则这条对角线叫做这个四边形的“巧分线”，这个四边形叫“巧妙四边形”，若一个四边形有两条巧分线，则称为“绝妙四边形．

1. 若四边形的一条对角线把四边形分成两个等腰三角形，则这条对角线叫做这个四边形的“巧分线”，这个四边形叫“巧妙四边形”，若一个四边形有两条巧分线，则称为“绝妙四边形．

(1) 下列四边形一定是巧妙四边形的是．（填序号）

①平行四边形；②矩形；③菱形；④正方形．

（初步应用）

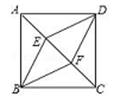
(2) 如图，在绝妙四边形ABCD中，AC＝AD，且AC垂直平分BD，若∠BAD＝80°，求∠BCD的度数．

(3) 在巧妙四边形ABCD中，AB＝AD＝CD，∠A＝90°，AC是四边形ABCD的巧分线，请直接写出∠BCD的度数．

【考点】

平行四边形的性质; 菱形的性质; 矩形的性质; 正方形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，E、F是正方形ABCD对角线AC上的两点，且AE＝EF＝FC，连接BE、DE、BF、DF．

(1) 求证：四边形BEDF是菱形：

(2) 求tan∠AFD的值．

综合题普通

2. 如图，已知正方形ABCD的边长为1，正方形CEFG的面积为 $\text{[math]}$ ，点E在CD边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为 $\text{[math]}$ ，且 $\text{[math]}$ .

(1) 求线段CE的长；

(2) 若点H为BC边的中点，连结HD，求证： $\text{[math]}$ .

综合题困难

3. 如图，在矩形ABCD中，BF⊥AC于点F，过点D作DE∥AC，过点A作AE⊥DE于点E，连结EF．

(1) 求证：四边形CDEF是平行四边形．

(2) 若AC=8，∠ACB=30°，则DE的长为。

综合题普通