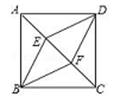
如图，E、F是正方形ABCD对角线AC上的两点，且AE＝EF＝FC，连接BE、DE、BF、DF．

1. 如图，在平面直角坐标系中，四边形 $\text{[math]}$ 为正方形，点 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 轴上，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ 两点，且与直线 $\text{[math]}$ 交于另一点 $\text{[math]}$ .

(1) 求抛物线的解析式；

(2) $\text{[math]}$ 为抛物线对称轴上一点， $\text{[math]}$ 为平面直角坐标系中的一点，是否存在以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是以 $\text{[math]}$ 为边的菱形.若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由；

(3) $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，过点 $\text{[math]}$ 作抛物线对称轴的垂线，垂足为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ .探究 $\text{[math]}$ 是否存在最小值.若存在，请求出这个最小值及点 $\text{[math]}$ 的坐标；若不存在，请说明理由.