如图，在△ABC中，AB＝2，BC＝4，△ABC的高AD与CE的比为（）

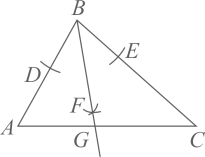
1. 如图，在△ABC中，AB＝2，BC＝4，△ABC的高AD与CE的比为（）

A. 1：2 B. 2：1 C. 1：4 D. 4：1

【考点】

三角形的面积;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，通过测量，并计算 $\text{[math]}$ 的面积，所得面积与下列数值最接近的是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式，称为海伦-秦九韶公式：如果一个三角形的三边长分别是a，b，c，记 $\text{[math]}$ ，那么三角形的面积为 $\text{[math]}$ .如图，在△ABC中，∠A，∠B，∠C所对的边分别记为a，b，c，若 $\text{[math]}$ ，则△ABC的面积为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. 18 D. $\text{[math]}$

单选题容易

3. 如图的4×4的方格纸中有一格点△ABC，其面积等于 $\text{[math]}$ cm² ，则这个方格纸的面积等于（）

A. 16cm² B. 20cm² C. 21cm² D. 24cm²

单选题容易