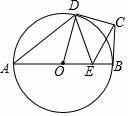
如图，AB为⊙O的直径，BC，CD是⊙O的切线，切点分别为点B，D，点E为线段OB上的一个动点，连接OD，CE，DE，已知AB＝2 ，BC＝2，当CE+DE的值最小时，则的值为（）

1. 如图，AB为⊙O的直径，BC，CD是⊙O的切线，切点分别为点B，D，点E为线段OB上的一个动点，连接OD，CE，DE，已知AB＝2 $\text{[math]}$ ，BC＝2，当CE+DE的值最小时，则 $\text{[math]}$ 的值为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

三角形的面积; 勾股定理; 轴对称的应用-最短距离问题; 两条直线被一组平行线所截，所得的对应线段成比例;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题困难

1. 在直角三角形中，若勾为3，股为4，则弦为（）

A. 5 B. 6 C. 7 D. 8

单选题容易

2. 如图，网格中每一小格的边长均为 1 ，点 $\text{[math]}$ 都在格点上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 直角三角形的两条直角边的长分别为6和8，则斜边长为（）

A. 10 B. 5 C. 4 D. 3

单选题容易