1.
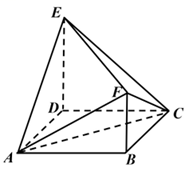
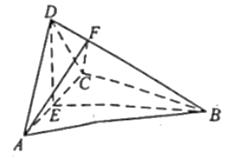
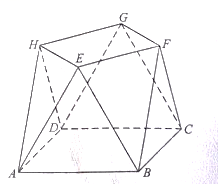
在棱长为2的正方体  中,(如图)
中,(如图)  是棱
是棱  的中点,
的中点,  是侧面
是侧面  的中心.
的中心.

(1)
求三棱锥  的体积;
(2)
求异面直线
的体积;
(2)
求异面直线  与
与  的夹角;
(3)
求
的夹角;
(3)
求  与底面
与底面  所成的角的大小.(结果用反三角函数表示)
所成的角的大小.(结果用反三角函数表示)
【考点】
棱柱、棱锥、棱台的体积;