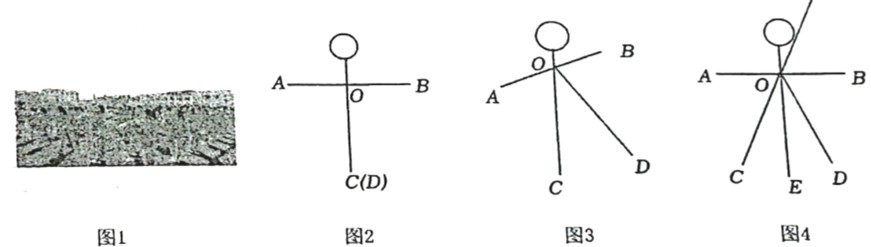
1.
已知 , 射线
, 射线 从与射线
从与射线 重合位置开始绕点O以每秒
重合位置开始绕点O以每秒 的速度按顺时针方向旋转,同时射线
的速度按顺时针方向旋转,同时射线 从与射线
从与射线 重合位置开始绕点O以每秒
重合位置开始绕点O以每秒 的速度按逆时针方向旋转,当射线
的速度按逆时针方向旋转,当射线 再次与射线
再次与射线 重合时.两条射线同时停止旋转,当
重合时.两条射线同时停止旋转,当 时,两条射线旋转的时间t的值为.
时,两条射线旋转的时间t的值为.

【考点】
一元一次方程的其他应用;
角的运算;
旋转的性质;
基础巩固
能力提升
变式训练
拓展培优