1.
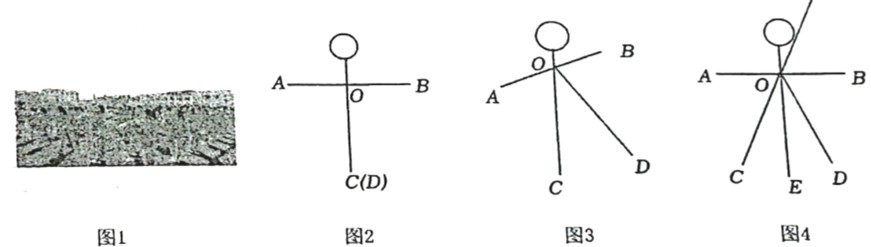
数学在我们生活中无处不在，一节广播操的运动过程就有数学问题．如图1为一节广播操动作的示意图，如图2，为了方便研究，两手手心位置分别记为A，B两点，两脚脚跟位置分别记为C，D两点，且A，B，C，D在同一个平面内，做操过程中将手脚运动近似看作A，B，C，D绕点O旋转，其中O为该平面内的一个定点．
(1)
如图2，A，O，B三点共线，且
， 则
°；
(2)
图3为腿部运动，A，O，B三点始终共线，却不在水平方向上，且
． 求
的值；
(3)
图4为体侧运动，在运动前A、O、B三点在同一水平线上，
， 
平分
且
， 
绕点O顺时针旋转，
的旋转速度为每秒
， 
的旋转速度为每秒
， 当旋转到与
重合时，运动停止．
①运动停止时，直接写出 ▲ °（用小于平角的度数表示）；
②判断运动过程中与
的数量关系，并说明理由．
【考点】
一元一次方程的其他应用;
角的运算;
角平分线的性质;
旋转的性质;
