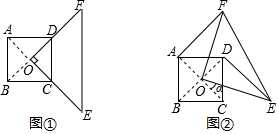1.
在正方形  中,点P是直线
中,点P是直线  上一点.连接
上一点.连接  ,将线段
,将线段  绕点P顺时针旋转
绕点P顺时针旋转  ,得到线段
,得到线段  ,连接
,连接  .
.

(1)
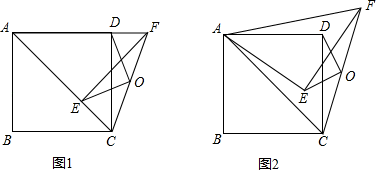
如图1.若点P在线段CB的延长线上过点E作  于H.与对角线AC交于点F.
(2)
若点P在射线
于H.与对角线AC交于点F.
(2)
若点P在射线  上,直接写出
上,直接写出  ,
,  ,
,  三条线段之间的数量关系(不必写过程).
三条线段之间的数量关系(不必写过程).
①请仔细阅读题目,根据题意在图上补全图形;②求证: .
【考点】
全等三角形的判定与性质;
正方形的性质;
旋转的性质;
等腰直角三角形;