1.
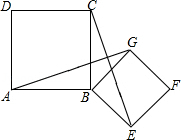
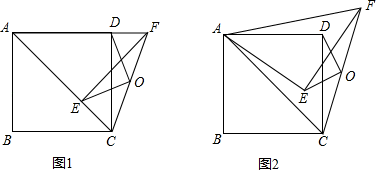
如图①,等腰直角三角形  的直角顶点
的直角顶点  为正方形
为正方形  的中心,点
的中心,点  ,
,  分别在
分别在  和
和  上,现将
上,现将  绕点
绕点  逆时针旋转
逆时针旋转  角
角  ,连接
,连接  ,
,  (如图②).
(如图②).
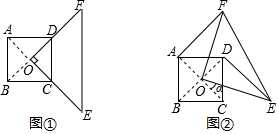
(1)
在图②中,  ;(用含
;(用含  的式子表示)
(2)
在图②中猜想
的式子表示)
(2)
在图②中猜想  与
与  的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
【考点】
全等三角形的判定与性质;
正方形的性质;
旋转的性质;
等腰直角三角形;