已知抛物线C：y2=8x的焦点为F，准线与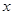轴的交点为K，点A在C上且，则的面积为()

1.

已知抛物线C：y²=8x的焦点为F，准线与轴的交点为K，点A在C上且 $\text{[math]}$ ，则 $\text{[math]}$ 的面积为()

A. 4　　 B. 8　　 C. 16　　 D. 32

【考点】

抛物线的定义; 抛物线的简单性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 已知 $\text{[math]}$ 是抛物线C： $\text{[math]}$ （ $\text{[math]}$ ）上的一点，F为抛物线C的焦点，且 $\text{[math]}$ ，则抛物线C的焦点坐标是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 已知抛物线 $\text{[math]}$ ： $\text{[math]}$ 上点 $\text{[math]}$ 的纵坐标为 $\text{[math]}$ ，则 $\text{[math]}$ 到 $\text{[math]}$ 的焦点的距离为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 已知点 $\text{[math]}$ 在拋物线 $\text{[math]}$ 上， $\text{[math]}$ 为 $\text{[math]}$ 的焦点，则 $\text{[math]}$ （）

A. $\text{[math]}$ B. 2 C. 3 D. $\text{[math]}$

单选题容易