1.
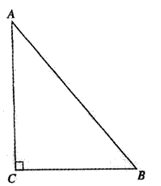
我们定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边的交点为勾股顶点.例如,在图1中,若CD是 中AB边上的高,且
中AB边上的高,且 , 则称
, 则称 为勾股高三角形,点
为勾股高三角形,点 为勾股顶点.
为勾股顶点.

(1)
【特例感知】
(2)
【深入探究】
(3)
【拓展应用】
如图1,CD是中AB边上的高,已知
, 请通过计算说明
是否是勾股高三角形.
如图2,已知为勾股高三角形,其中点
为勾股顶点,且
是AB边上的高.探究线段AD与BC的数量关系,并给予证明.
如图3,为勾股高三角形,其中
为勾股顶点,且
为AB边上的高,过点
作
, 垂足分别为E,F.若
, 求
的值.
【考点】
三角形的面积;
勾股定理;
能力提升
真题演练