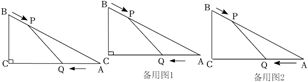
1.
在平面直角坐标系中,已知 , 点
, 点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 的速度移动;点
的速度移动;点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 的速度移动.如果
的速度移动.如果 同时出发,用
同时出发,用 表示移动的时间
表示移动的时间 ,
,

(1)
用含 的代数式表示:线段
的代数式表示:线段
 ;
;
 .
(2)
当
.
(2)
当 为何值时
为何值时 的面积为
的面积为 ?
(3)
当
?
(3)
当 与
与 相似时,求出
相似时,求出 的值.
的值.
【考点】
三角形-动点问题;
能力提升
真题演练