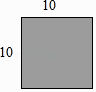
1.
如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以4cm/秒的速度由B点向C点运动,同时,点Q在线段CD上以acm/秒的速度由C点向D点运动,设运动的时间为t秒,
(1)CP的长为 cm(用含t的代数式表示);
(2)若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,求a的值.
(3)若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动.则点P与点Q会不会相遇?若不相遇,请说明理由.若相遇,求出经过多长时间点P与点Q第一次在正方形ABCD的何处相遇?

【考点】
正方形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练