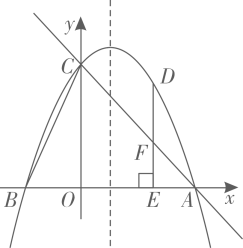
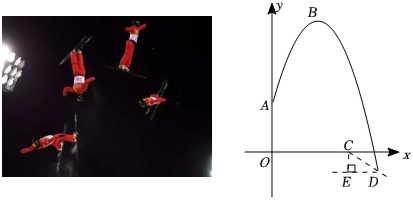
如图，某跳水运动员在10米跳台上进行跳水训练，水面边缘点E坐标为（﹣1，﹣10），运动员（将运动员看成一点）在空中运动的路线是经过原点O的抛物线．在跳某个规定动作时，运动员在空中最高处A点的坐标为，正常情况下，运动员在距水面高度5米之前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误，运动员入水后，运动路线为另一条抛物线．

1. 如图，某跳水运动员在10米跳台上进行跳水训练，水面边缘点E坐标为（﹣1，﹣10），运动员（将运动员看成一点）在空中运动的路线是经过原点O的抛物线．在跳某个规定动作时，运动员在空中最高处A点的坐标为 $\text{[math]}$ ，正常情况下，运动员在距水面高度5米之前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误，运动员入水后，运动路线为另一条抛物线．

(1) 求运动员在空中运动时对应抛物线的解析式，并求出入水处点B的坐标．

(2) 若运动员在空中调整好入水姿势时，恰好距点E的水平距离为4米，问该运动员此次跳水会不会失误？通过计算说明理由．

(3) 在该运动员入水点的正前方有M ， N两点，且EM＝7，EN＝9，该运动员入水后运动路线对应的抛物线解析式为y＝（x﹣h）²+k ，若该运动员出水点D在MN之间（包括M ， N两点），则k的取值范围是．

【考点】

待定系数法求二次函数解析式;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. “闻起来臭，吃起来香”的臭豆腐是长沙特色小吃，臭豆腐虽小，但制作流程却比较复杂，其中在进行加工煎炸臭豆腐时，我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”，在特定条件下，“可食用率”p与加工煎炸的时间t（单位：分钟）近似满足函数关系式： $\text{[math]}$ （ $\text{[math]}$ a，b，c为常数），如图纪录了三次实验数据，根据上述函数关系和实验数据，可以得到加工煎炸臭豆腐的最佳时间为（）

A. 3.50分钟 B. 4.05分钟 C. 3.75分钟 D. 4.25分钟

单选题普通

2. 如图，抛物线y＝ax²+bx+2与x轴交于A，B两点，且OA＝2OB，与y轴交于点C，连接BC，抛物线对称轴为直线x＝ $\text{[math]}$ ，D为第一象限内抛物线上一动点，过点D作DE⊥OA于点E，与AC交于点F，设点D的横坐标为m．

(1) 求抛物线的表达式；

(2) 当线段DF的长度最大时，求D点的坐标；

(3) 抛物线上是否存在点D，使得以点O，D，E为顶点的三角形与 $\text{[math]}$ 相似？若存在，求出m的值；若不存在，请说明理由．

综合题困难

3. $\text{[math]}$ 北京冬奥会自由式滑雪空中技巧比赛中，某运动员比赛过程的空中剪影近似看作一条抛物线，跳台高度 $\text{[math]}$ 为4米，以起跳点正下方跳台底端 $\text{[math]}$ 为原点，水平方向为横轴，竖直方向为纵轴，建立如图所示平面直角坐标系．已知抛物线最高点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，着陆坡顶端 $\text{[math]}$ 与落地点 $\text{[math]}$ 的距离为2.5米，若斜坡 $\text{[math]}$ 的坡度 $\text{[math]}$ （即 $\text{[math]}$ ）．求：

(1) 点 $\text{[math]}$ 的坐标；

(2) 该抛物线的函数表达式；

(3) 起跳点 $\text{[math]}$ 与着陆坡顶端 $\text{[math]}$ 之间的水平距离 $\text{[math]}$ 的长．（精确到0.1米）（参考数据： $\text{[math]}$ ）

综合题普通