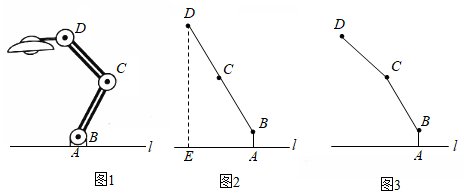
1.
图①是某种可调节支撑架, 为水平固定杆,竖直固定杆
为水平固定杆,竖直固定杆 , 活动杆
, 活动杆 可绕点A旋转,
可绕点A旋转, 为液压可伸缩支撑杆,已知
为液压可伸缩支撑杆,已知 ,
,  ,
,  .
.

(1)
如图②,当活动杆 处于水平状态时,求可伸缩支撑杆
处于水平状态时,求可伸缩支撑杆 的长度(结果保留根号);
(2)
如图③,当活动杆
的长度(结果保留根号);
(2)
如图③,当活动杆 绕点A由水平状态按逆时针方向旋转角度
绕点A由水平状态按逆时针方向旋转角度 , 且
, 且 (
( 为锐角),求此时可伸缩支撑杆
为锐角),求此时可伸缩支撑杆 的长度(结果保留根号).
的长度(结果保留根号).
【考点】
矩形的判定与性质;
解直角三角形的其他实际应用;