1.
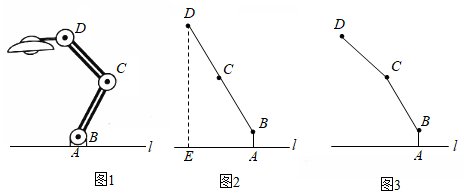
“五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直
, 用绳子拉直 后系在树干
后系在树干 上的点
上的点 处,使得
处,使得 ,
,  ,
,  在一条直线上,通过调节点
在一条直线上,通过调节点 的高度可控制“天幕”的开合,
的高度可控制“天幕”的开合, m,
m, m.
m.

(参考数据: ,
,
,
)
(1)
天晴时打开“天幕”,若 , 求遮阳宽度
, 求遮阳宽度 (结果精确到0.1m);
(2)
下雨时收拢“天幕”,
(结果精确到0.1m);
(2)
下雨时收拢“天幕”, 从65°减少到45°,求点
从65°减少到45°,求点 下降的高度(结果精确到0.1m).
下降的高度(结果精确到0.1m).
【考点】
矩形的判定与性质;
解直角三角形的其他实际应用;
能力提升
真题演练