1.
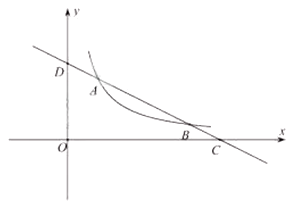
如图,在平面直角坐标系 中,直线
中,直线 分别交
分别交 轴和
轴和 轴于点A,B,直线
轴于点A,B,直线 交
交 轴正半轴于点C,交
轴正半轴于点C,交 于点
于点 ,
,  .
.

(1)
求直线 的函数解析式;
(2)
若P是直线
的函数解析式;
(2)
若P是直线 上一点,且使得
上一点,且使得 , 直接写出点P的坐标.
, 直接写出点P的坐标.
【考点】
待定系数法求一次函数解析式;