1.
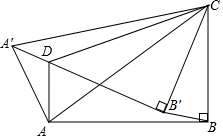
如图,将 绕点
绕点 逆时针旋转
逆时针旋转 至
至 的位置,此时A、B、D三点共线.
的位置,此时A、B、D三点共线.

(1)
求 的大小;
(2)
若
的大小;
(2)
若 ,
,  , 求
, 求 的长.
的长.
【考点】
等腰三角形的性质;
勾股定理;
旋转的性质;