1.
在如图所示的实验装置中,两个正方形框架 ,
,  的边长都是1,且他们所在的平面互相垂直,活动弹子
的边长都是1,且他们所在的平面互相垂直,活动弹子 ,
,  分别在正方形对角线
分别在正方形对角线 和
和 上移动,且
上移动,且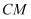 和
和 的长度保持相等,及
的长度保持相等,及

(1)
求 的长;
(2)
的长;
(2)
 为何值时,
为何值时, 的长最小,最小值是多少?
(3)
当
的长最小,最小值是多少?
(3)
当 的长最小时,求平面
的长最小时,求平面 与平面
与平面 的夹角的余弦值.
的夹角的余弦值.
【考点】
函数的最大(小)值;
空间中两点间的距离公式;
用空间向量研究二面角;


