已知：在△ABC中，E是AC上一点，∠AEB=∠ABC.

1. 已知：在△ABC中，E是AC上一点，∠AEB=∠ABC.

(1) 如图①，作∠BAC的角平分线AD，分别交CB，BE于点D，F.

求证：∠EFD=∠ADC.

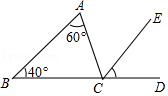
(2) 如图②，作△ABC的外角∠BAG的角平分线AD，直线AD分别交CB，BE的延长线于点D，F.试探究(1)中的结论是否仍然成立，并说明理由.

【考点】

三角形的外角性质; 角平分线的概念;

【答案】

您现在未登录，无法查看试题答案与解析。登录

证明题普通

证明题普通

证明题普通

3. 如图，已知 $\text{[math]}$ ， $\text{[math]}$ 在三角形 $\text{[math]}$ 的边 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ 。
求证： $\text{[math]}$

证明题普通