已知：在△ABC中，∠BAC=90°，AB=AC.AE是过点A的一条直线，BD⊥AE于点D，CE⊥AE于点E.

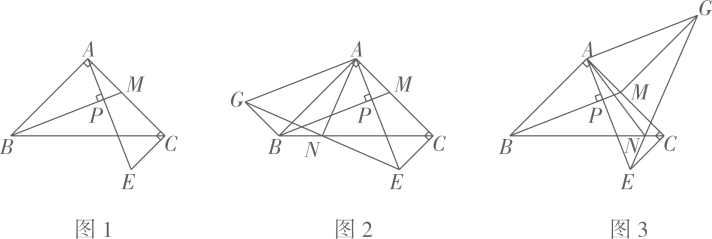
1. 已知：在△ABC中，∠BAC=90°，AB=AC.AE是过点A的一条直线，BD⊥AE于点D，CE⊥AE于点E.

(1) 若点B，C在AE的同侧，如图①.

①求证：△ABD≌△CAE.

②BD+CE=DE成立吗?为什么?

(2) 若B，C在AE的异侧，如图②，其他条件不变，则BD，DE与CE有怎样的数量关系?直接写出结果.

【考点】

三角形全等的判定-ASA; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，

(1) 求证： $\text{[math]}$ ≌ $\text{[math]}$ ；

(2) 猜想： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的数量关系为 $\text{[math]}$ 不需证明 $\text{[math]}$ ；

(3) 当 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转到图 $\text{[math]}$ 位置时，猜想线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间又有怎样的数量关系，并证明你的结论．

解答题普通

2. 在一款电子游戏中，游戏中的小精灵到达一个高为10米的高台A，利用旗杆顶部(O)的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B.求旗杆(OM)的高度.

解答题普通

3. 如图，在 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

解答题普通