1.
已知正方形  ,
,  ,
,  为平面内两点.
为平面内两点.

(1)
(探究建模)
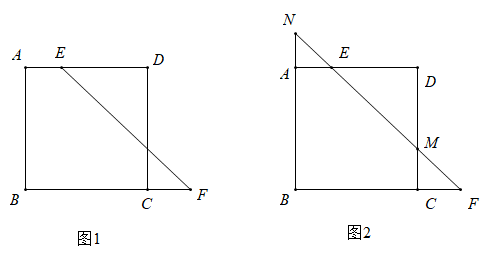
如图1,当点 在边
在边  上时,
上时,  ,且
,且  ,
,  ,
,  三点共线.求证:
三点共线.求证:  ;
(2)
(类比应用)
;
(2)
(类比应用)
如图2,当点 在正方形
在正方形  外部时,
外部时,  ,
,  ,且
,且  ,
,  ,
,  三点共线.猜想并证明线段
三点共线.猜想并证明线段  ,
,  ,
,  之间的数量关系;
(3)
(拓展迁移)
之间的数量关系;
(3)
(拓展迁移)
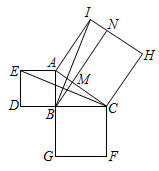
如图3,当点 在正方形
在正方形  外部时,
外部时,  ,
,  ,
,  ,且
,且  ,
,  ,
,  三点共线,
三点共线,  与
与  交于
交于  点.若
点.若  ,
,  ,求
,求  的长.
的长.
如图1,当点
如图2,当点
如图3,当点
【考点】
勾股定理;
正方形的性质;
等腰直角三角形;
三角形全等的判定-ASA;
三角形全等的判定-AAS;