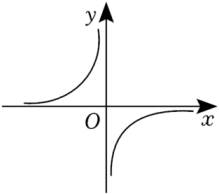
已知反比例函数，分别根据下列条件求出字母的取值范围：(1)函数图象位于第一、三象限；（2）在每一象限内，随的增大而增大.

1. 已知反比例函数 $\text{[math]}$ ，分别根据下列条件求出字母 $\text{[math]}$ 的取值范围：(1)函数图象位于第一、三象限；（2）在每一象限内， $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大.

【考点】

反比例函数的图象; 反比例函数的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 若点A(−1，y₁)，B(1，y₂)，C(2，y₃)都在反比例函数 $\text{[math]}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是．

填空题容易

2. 已知反比例函数 $\text{[math]}$ （m是常数）的图象在第二、四象限，求m的取值范围．

解答题容易

3. 在反比例函数 $\text{[math]}$ 图象的每一条曲线上，y随x的增大而减小．

（1）函数经过哪些象限？

（2）求 $\text{[math]}$ 的取值范围．

解答题容易