1.
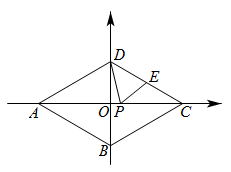
如图,P为∠AOB内一定点,∠AOB=45°,M、N分别是射线OA、OB上任意一点,当△PMN周长的最小值为10时,则O、P两点间的距离为.

【考点】
两点之间线段最短;
基础巩固
能力提升
变式训练
拓展培优
真题演练