1.
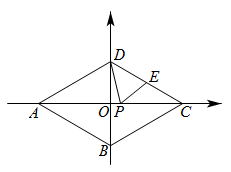
如图,在四边形ABCD 内找一点O,使它与四边形四个顶点的距离的和 
 最小,并说出你的理由. 由本题你得到什么数学结论? 举例说明它在实际中的应用.
最小,并说出你的理由. 由本题你得到什么数学结论? 举例说明它在实际中的应用.

【考点】
两点之间线段最短;
基础巩固
能力提升
变式训练
拓展培优
真题演练